Navigation

Condenser Area Derivation

For a configuration like the cross-flow Condenser, the area on both refrigerant and air sides is proportional to a parameter 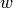w, the length fraction for a given circuit. In addition, the air mass flow rate is proportional to the parameter 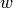w. As a result, independent of whether the minimum capacitance rate is on the air- or refrigerant-side, the same result for the area fraction 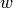w is obtained, as shown from the derivation below.

For this derivation, the inlet temperatures of both streams are known, and the outlet stream of the refrigerant is known. In addition, the mass flow rates of refrigerant and air are known. Therefore, the actual amount of heat transfer is also known.

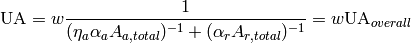
(1)\mathrm{UA} =w\dfrac{1}{ (\eta_a \alpha_a A_{a,total})^{-1} + (\alpha_{r} A_{r,total})^{-1}}=w\mathrm{UA}_{overall}\\

Minimum capacitance rate on air side

If C_{min} on air side:

(2)\mathrm{Ntu} = \frac{\mathrm{UA}}{wc_{p,a} \dot m_{a,total}}=\frac{\mathrm{UA}_{overall}}{c_{p,a}\dot m_{a,total}}

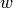w cancels out, leaving 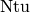\mathrm{Ntu} independent of 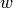w. Energy balance yields

(3)\dot m_rc_{p,r}(T_{r,i}-T_{r,o})=\varepsilon C_{min} (T_{r,i}-T_{a,i})

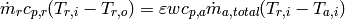
(4)\dot m_rc_{p,r}(T_{r,i}-T_{r,o})=\varepsilon w c_{p,a} \dot m_{a,total} (T_{r,i}-T_{a,i})

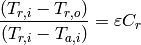
(5)\frac{(T_{r,i}-T_{r,o})}{(T_{r,i}-T_{a,i})}=\varepsilon C_r

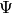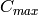LHS is constant, call it \Psi. The minimum capacitance rate is on the air side (C_{min}= w\dot m_{a,total} c_{p,a} ), cross-flow with C_{max} mixed (ref.) and C_{min} unmixed (air) yields

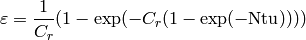
(6)\varepsilon = \displaystyle\frac{1}{C_r} (1 - \exp(-C_r (1 - \exp(-\mathrm{Ntu}))))\\

Now solve for 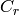C_r

(7)\Psi = (1 - \exp(-C_r (1 - \exp(-\mathrm{Ntu}))))\\

(8)\exp(-C_r (1 - \exp(-\mathrm{Ntu}))) = 1 - \Psi\\

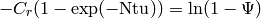
(9)-C_r (1 - \exp(-\mathrm{Ntu})) = \ln(1 - \Psi)\\

(10)C_r = -\frac{\ln(1 - \Psi)}{(1 - \exp(-\mathrm{Ntu}))}

Coming back to the definition of 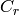C_r as the ratio of capacitance rates, you can get 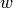w from

(11)w=C_r\frac{\dot m_rc_{p,r}}{\dot m_{a,total} c_{p,a}}

and since 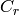C_r is already known, you obtain

(12)w=-\frac{\ln(1 - \Psi)}{(1 - \exp(-\mathrm{Ntu}))} \frac{\dot m_rc_{p,r}}{\dot m_{a,total} c_{p,a}}

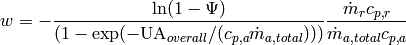
(13)w=-\frac{\ln(1 - \Psi)}{(1 - \exp(-\mathrm{UA}_{overall}/(c_{p,a}\dot m_{a,total})))} \frac{\dot m_rc_{p,r}}{\dot m_{a,total} c_{p,a}}

Minimum capacitance rate on refrigerant side

If C_{min} on refrigerant side:

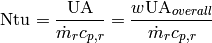
(14)\mathrm{Ntu} = \frac{\mathrm{UA}}{\dot m_r c_{p,r}}=\frac{w\mathrm{UA}_{overall}}{\dot m_r c_{p,r}}

(15)C_r\mathrm{Ntu} = \frac{\dot m_r c_{p,r}}{w\dot m_{a,total} c_{p,a}}\frac{w\mathrm{UA}_{overall}}{\dot m_r c_{p,r}}

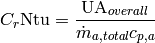
(16)C_r\mathrm{Ntu} = \frac{\mathrm{UA}_{overall}}{\dot m_{a,total} c_{p,a}}

Energy balance yields

(17)\dot m_rc_{p,r}(T_{r,i}-T_{r,o})=\varepsilon C_{min} (T_{a,i}-T_{r,i})

(18)\dot m_rc_{p,r}(T_{r,i}-T_{r,o})=\varepsilon\dot m_rc_{p,r} (T_{a,i}-T_{r,i})

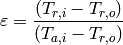
(19)\varepsilon=\frac{(T_{r,i}-T_{r,o})}{(T_{a,i}-T_{r,o})}

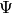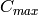Right-hand-side is also equal to \Psi from above. Effectiveness with C_{min} mixed (ref.) and C_{max} unmixed (air) yields

(20)\varepsilon = 1 - \exp(-\displaystyle\frac{1}{C_r} (1 - \exp(-C_r \mathrm{Ntu})))

(21)\exp(-\displaystyle\frac{1}{C_r} (1 - \exp(-C_r \mathrm{Ntu}))) = 1 - \varepsilon

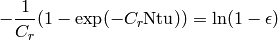
(22)-\dfrac{1}{C_r} (1 - \exp(-C_r \mathrm{Ntu})) = \ln(1 - \epsilon)

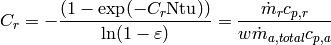
(23){C_r}=-\frac{ (1 - \exp(-C_r \mathrm{Ntu}))}{\ln(1 - \varepsilon)}=\frac{\dot m_r c_{p,r}}{w\dot m_{a,total} c_{p,a}}

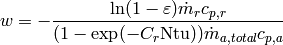
(24)w=-\frac{\ln(1 - \varepsilon)\dot m_r c_{p,r}}{ (1 - \exp(-C_r \mathrm{Ntu}))\dot m_{a,total} c_{p,a}}

(25)w=-\frac{\ln(1 - \Psi)\dot m_r c_{p,r}}{ [1 - \exp(-\mathrm{UA}_{overall}/(c_{p,a}\dot m_{a,total}))]\dot m_{a,total} c_{p,a}}

Thus both assuming that the minimum capacitance rate is on the air- or refrigerant-sides yields exactly the same solution, which conveniently allows for an explicit solution independent of whether the air-side is the limiting capacitance rate or not

Table Of Contents

Previous topic

Appendices

Next topic

Algorithm of partial-wet-partial-dry evaporator

This Page

Navigation

© Copyright 2011, Ian Bell. Created using Sphinx 1.1.3.