Navigation

Compressor

Overview

A compressor is the heart of the air-conditioning or refrigeration system, compressing the refrigerant from the low-pressure side of the system up to the high-pressure side of the system. Because it plays such a a significant role in the overall system efficiency, the accuracy of the compressor model is quite important.

Mathematical Description

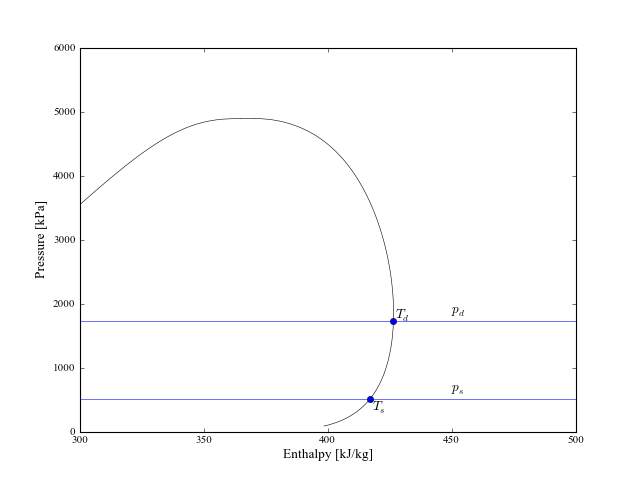
The compressor is modeled based on a 10-coefficient ARI compressor map which is very commonly used to characterize the performance of compressors. The map is based on a given amount of superheat along with input saturated suction and discharge pressures. Though most everything else in the program is based on metric units, the standard in America is to generate the map based on superheat and saturated temperatures in degrees Fahrenheit. Refer to the following figure to see the definitions of the temperatures and pressures:

(Source code, png, hires.png, pdf)

../_images/Compressor-1.png

Thus the map-based mass flow rate (in lbm/hr) and electrical power (in W), can be given by

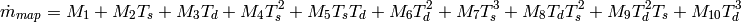
(1)\dot {m}_{map} = M_{1}+M_{2}T_s+M_{3}T_{d}+M_{4}T_{s}^2+M_{5}T_{s}T_d+M_{6}T_{d}^2+M_{7}T_{s}^3+M_{8}T_{d}T_{s}^2+M_{9}T_{d}^{2}T_{s}+M_{10}T_{d}^3

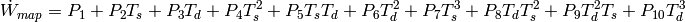
(2)\dot W_{map} = P_{1}+P_{2}T_s+P_{3}T_{d}+P_{4}T_{s}^2+P_{5}T_{s}T_d+P_{6}T_{d}^2+P_{7}T_{s}^3+P_{8}T_{d}T_{s}^2+P_{9}T_{d}^{2}T_{s}+P_{10}T_{d}^3

where the saturated suction dewpoint temperature 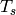T_s and saturated discharge dewpoint temperatures 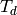T_d are in degrees Fahrenheit. To be specific, they are the dew temperatures, which are the same as the saturated vapor temperatures for pure fluids. The coefficients 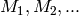M_1, M_2, ... are the mass flow map coefficients and 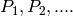P_1, P_2, .... are the electrical power map coefficients. In practice, the compressor is unlikely to operate at exactly the map superheat. As a result, the map predictions must be corrected to better match the actual operating conditions. The map correction is based on the method of Rice. et al. [1] , which yields

(3)\dot m_{actual} = \left[1 + 0.75 \left(\frac{v_{map}}{ v_{actual}} - 1\right ) \right ] \dot m_{map}

where the subscripts actual refer to the properties evaluated at the actual superheat at the suction flange, and the map subscripts refer to the properties evaluated at the given map superheat. Similarly, the electrical power correction is given by

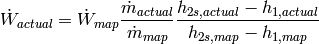
(4)\dot W_{actual} = \dot W_{map} \frac{\dot m_{actual}}{ \dot m_{map}} \frac{ h_{2s,actual} - h_{1,actual}}{h_{2s,map} - h_{1,map}}

An energy balance over the compressor yields

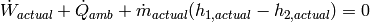
(5)\dot W_{actual}+\dot Q_{amb}+\dot m_{actual}(h_{1,actual}-h_{2,actual})=0

Since the electrical power is known from the corrected map, and the heat transfer can be expressed as a fraction of the electrical power by

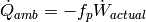
(6)\dot Q_{amb}=-f_p\dot W_{actual}

the outlet enthalpy of the compressor can be therefore given by

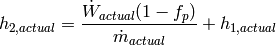
(7)h_{2,actual}=\frac{\dot W_{actual}(1-f_p)}{\dot m_{actual}}+h_{1,actual}

References

[1]Rice, C. K. and A. E. Dabiri, 1981. “A Compressor Simulation Model with Corrections for the Level of Suction Gas Superheat,” ASHRAE Transactions, Vol. 87, Part 2, pp.771-782.

Nomenclature

Variable Description
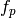f_p Fraction of electrical power lost at heat transfer [-]
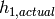h_{1,actual} Enthalpy of refrigerant at actual superheat [J/kg]
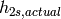h_{2s,actual} Isentropic enthalpy of refrigerant at discharge pressure using actual superheat [J/kg]
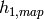h_{1,map} Enthalpy of refrigerant at map superheat [J/kg]
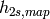h_{2s,map} Isentropic enthalpy of refrigerant at discharge pressure using map superheat [J/kg]
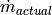\dot m_{actual} Actual refrigerant mass flow rate [kg/s]
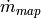\dot m_{map} Refrigerant mass flow rate from map [lbm/hr]
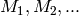M_1,M_2,... Mass flow map coefficients [varied]
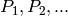P_1,P_2,... Electrical power map coefficients [varied]
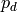p_d Discharge dew pressure [kPa (absolute)]
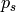p_s Suction dew pressure [kPa (absolute)]
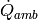\dot Q_{amb} Ambient heat loss [W]
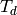T_d Discharge dew temperature [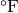^{\circ}\mathrm{F}]
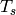T_s Suction dew temperature [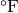^{\circ}\mathrm{F}]
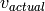v_{actual} Specific volume of refrigerant at actual superheat [m3/kg]
v_{map} Specific volume of refrigerant at map superheat [m3/kg]
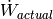\dot W_{actual} Actual compressor electrical power [W]
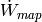\dot W_{map} Compressor electrical power from map [W]

Compressor Sample Code

Minimal Component Test:

from Compressor import CompressorClass
from CoolProp.CoolProp import Props
kwds={
      'M':[217.3163128,5.094492028,-0.593170311,4.38E-02,
        -2.14E-02,1.04E-02,7.90E-05,-5.73E-05,1.79E-04,-8.08E-05],
      'P':[-561.3615705,-15.62601841,46.92506685,-0.217949552,
        0.435062616,-0.442400826,2.25E-04,2.37E-03,-3.32E-03,2.50E-03],
      'Ref':'R134a',
      'Tin_r':280,
      'pin_r':Props('P','T',279,'Q',1,'R134a'),
      'pout_r':Props('P','T',315,'Q',1,'R134a'),
      'fp':0.15, #Fraction of electrical power lost as heat to ambient
      'Vdot_ratio': 1.0 #Displacement Scale factor
      }
Comp=CompressorClass(**kwds)
Comp.Calculate()

print 'Electrical power is: ' + str(Comp.W) + ' W'
print 'Actual mass flow rate is: ' + str(Comp.mdot_r) + ' kg/s'

If you open an IPython(x,y) shell in the root of the documentation (folder Documentation/Web relative to the main trunk), and run the commands below, you should get

In [2]: execfile('ACHPComponents/ComponentTests/CompressorTest.py')
Electrical power is: 2295.80966961 W
Actual mass flow rate is: 0.0626893978315 kg/s

If not, first stop should be the Frequently Asked Questions

Component Class Documentation

class Compressor.CompressorClass(**kwargs)[source]

Compressor Model based on 10-coefficient Model from ANSI/AHRI standard 540

Required Parameters:

Variable Units Description
M varied A numpy-like list of compressor map coefficients for mass flow
P varied A numpy-like list of compressor map coefficients for electrical power
Ref N/A A string representing the refrigerant
Tin_r K Refrigerant inlet temperature
pin_r kPa Refrigerant suction pressure (absolute)
pout_r kPa Refrigerant discharge pressure (absolute)
fp – Fraction of electrical power lost as heat to ambient
Vdot_ratio – Displacement Scale factor

All variables are of double-type unless otherwise specified

Calculate()[source]
OutputList()[source]

Return a list of parameters for this component for further output

It is a list of tuples, and each tuple is formed of items with indices:

[0] Description of value

[1] Units of value

[2] The value itself

Update(**kwargs)[source]

Table Of Contents

Previous topic

ACHP Component Models

Next topic

Fin-Tube Heat Exchangers

This Page

Navigation

© Copyright 2011, Ian Bell. Created using Sphinx 1.1.3.